已知盒中有10个灯泡,其中8个正品,2个次品。需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止。设ξ为取出的次数,求P(ξ=4)=
A.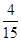 |
B.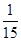 |
C.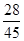 |
D.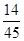 |
如图;现有一迷失方向的小青蛙在3处,它每跳动一次可以等机会地进入相邻的任意一格(如若它在5处,跳动一次,只能进入3处,若在3处,则跳动一次可以等机会进入l,2,4,5处),则它在第三次跳动后,进入5处的概率是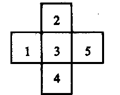
A.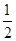 |
B.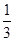 |
C.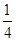 |
D.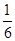 |
箱中装有标号为1,2,3,4,5,6且大小相同的6个球,从箱中一次摸出两个球,记下号码并放回,如果两球号码之积是4的倍数,则获奖.现有4人参与摸奖,恰好有3人获奖的概率是
A. |
B. |
C. |
D. |
在15个村庄中,有7个村庄交通不太方便,现从中任意选10个村庄,用X表示10个村庄中交通不太方便的村庄数,下列概率中等于 的是( )
的是( )
A. |
B. |
C. |
D. |
箱中有5个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中重新取球,若取出白球,则停止取球,那么在第四次取球之后停止的概率为( )
A.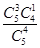 |
B.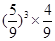 |
C.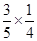 |
D.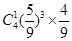 |
掷两颗骰子,所得点数之和为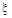 ,那么
,那么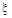 =4表示的随机试验结果是( )
=4表示的随机试验结果是( )
| A.一颗是3点,一颗是1点 | B.两颗都是2点 |
| C.两颗都是4点 | D.一颗是3点,一颗是1点或两颗都是2点 |
某种种子每粒发芽的概率都为0.9,现播种了1 000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的均值为( )
| A.100 | B.200 | C.300 | D.400 |