设随机变量 服从分布B(n,p),且E
服从分布B(n,p),且E =1.6,D
=1.6,D =1.28则( )
=1.28则( )
| A.n=4,p="0.4" | B.n=5,p=0.32 | C.n=8,p=0.2 | D.n=7,p=0.45 |
为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
| |
做不到“光盘” |
能做到“光盘” |
| 男 |
45 |
10 |
| 女 |
30 |
15 |
附:
P(K2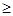 k) k) |
0.10 |
0.05 |
0.025 |
| k |
2.706 |
3.841 |
5.024 |

参照附表,得到的正确结论是( )
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”
掷两颗骰子,所得点数之和为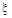 ,那么
,那么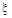 =4表示的随机试验结果是( )
=4表示的随机试验结果是( )
| A.一颗是3点,一颗是1点 | B.两颗都是2点 |
| C.两颗都是4点 | D.一颗是3点,一颗是1点或两颗都是2点 |
已知随机变量ξ的概率分布如下:
| ξ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| P |
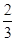 |
 |
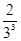 |
 |
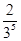 |
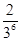 |
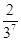 |
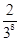 |
 |
m |
则P(ξ=10)等于( )
A、 B、
B、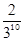 C、
C、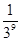 D.、
D.、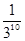
在三次独立重复试验中,事件A在每次试验中发生的概率相同,若事件A至少发生一次的概率为 ,则事件A恰好发生一次的概率为( )
,则事件A恰好发生一次的概率为( )
A. |
B. |
C. |
D. |
某种种子每粒发芽的概率都为0.9,现播种了1 000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的均值为( )
| A.100 | B.200 | C.300 | D.400 |
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3。设各车主购买保险相互独立.
(Ⅰ)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(Ⅱ)求该地3位车主中恰有1位车主甲、乙两种保险都不购买的概率.
随机变量ξ的概率分布列为P(ξ=n)=a( )n(n=0.1.2),其中a为常数,列P(0.1<ξ<2.9)的值为
)n(n=0.1.2),其中a为常数,列P(0.1<ξ<2.9)的值为
A. . . |
B. |
C. |
D. |