高中数学向量的概念选择题

已知四边形ABCD的三个顶点，，，且，则顶
点D的坐标为（  ）

A．

B．

C．

D．

已知平面向量，，且，则的值为（   ） 

A．－3

B．-1

C．1

D．3

已知向量，若，则_____

给出下列命题：
（1）两个具有公共终点的向量，一定是共线向量。
（2）两个向量不能比较大小，但它们的模能比较大小。
（3）a=0（为实数），则必为零。
（4），为实数，若a=b，则a与b共线。
其中错误的命题的个数为 

A．1

B．2

C．3

D．4

若，且的夹角为钝角，则x的取值范围是（   ）

A．

B．

C．

D．

已知向量，，．若为实数，，则        。

已知平面向量，，且，则  （   ）

A．

B．

C．

D．

若平行四边形的3个顶点分别是（4，2），（5，7），（3，4），则第4个顶点的坐标不可能是（  ）

A．（12，5）

B．（-2，9）

C．（3，7）

D．（-4，-1）

设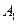，，，是平面直角坐标系中两两不同的四点，若 (λ∈R)，(μ∈R)，且,则称，调和分割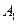， ,已知点C(c，o),D(d，O) (c，d∈R)调和分割点A(0，0)，B(1，0)，则下面说法正确的是（  ）

A．C可能是线段AB的中点	B．D可能是线段AB的中点
C．C，D可能同时在线段AB上	D．C，D不可能同时在线段AB的延长线上

已知均为单位向量，它们的夹角为，那么（ ）

A．

B．

C．

D．

设a,b是不共线的两个向量,其夹角是θ,若函数f(x)=(xa+b)·(a-xb)(x∈R)在(0,+∞)上有最大值,则(　　)

A．|a|<|b|,且θ是钝角

B．|a|<|b|,且θ是锐角

C．|a|>|b|,且θ是钝角

D．|a|>|b|,且θ是锐角

设是两个非零向量，下列选项正确的是（   ）

A．若，则

B．若，则

C．若，则存在实数，使得

D．若存在实数，使得，则

若两个非零向量满足，则向量与的夹角为（    ）

A．

B．

C．

D．

如图，向量-等于   (       )

A．

B．

C．

D．

已知四边形是菱形，点在对角线上（不包括），则（　　）

A．	B．
C．	D．