初中数学圆幂定理试题

某课题小组研究如下的几个问题．
（1）边长为1的等边三角形从图1位置开始沿直线顺时针无滑动地向右滚动一周，求点P运动的路径长（直接列式计算）；
（2）边长为1的正方形从图2位置开始沿直线顺时针无滑动地向右滚动，当正方形滚动一周时，求点P运动的路经长（直接列式计算）．
（3）请你将（1）（2）中的正多边形化成一个边长为1，边数大于4的正多边形，按（1）（2）的方式滚动一周，求其任意一个顶点运动的路径长（请写出你选的图形的名称，直接写出结果）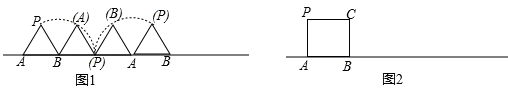

如图，在△ABC中，AB=AC，∠ABC=30°，点O在边BC上，⊙O经过点A，B，且与BC相交于点D．

（1）求证：CA是⊙O的切线；
（2）若AB=2，请直接写出阴影部分的面积．

如图，⊙O是△ABC的外接圆，半径为4，直线l与⊙O相切，切点为P，l∥BC，l与BC间的距离为7．

（1）仅用无刻度的直尺，画出一条弦，使这条炫将△ABC分成面积相等的两部分（保留作图痕迹，不写画法）．
（2）求弦BC的长．

如图，四边形ABCD内接于⊙O，∠DAE是四边形ABCD的一个外角，且AD平分∠CAE．
求证：DB=DC．

已知△ABC，∠C=90°，AC=4，BC=3．
（1）用尺规在图1中作出△ABC的外接圆，在图2中作出△ABC的内切圆．
（2）△ABC的外接圆半径为        ，内切圆半径为         ．

同圆的内接正方形和内接正三角形的边长比是                  ．

将量角器按如图所示的方式放置在三角形纸片上，使点O在半圆上，点B在半圆上，边AB，AO分别交半圆于点C，D，点B，C，D对应的读数分别为160°、52°、40°，则∠A=       ．

如图，AB为⊙O直径，点C，D在⊙O上，若∠DCB=30°，则∠DBA=             ．

将圆心角为90°，面积为4π的扇形围成一个圆锥的侧面，则所围成的圆锥的底面半径为                      ．

已知⊙A的半径是6，点A的坐标是（-3，-4），那么⊙A与x轴的位置关系是        ．

已知⊙O的半径是3，OP=2，则点P与⊙O的位置关系是：点P在⊙O              ．

如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E，F，∠E=α，∠F=β，则∠A=（    ）

A．α+β

B．

C．180-α-β

D．

如图，四边形ABCD为⊙O的内接四边形，已知∠BOD=100°，则∠BCD的度数为（    ）

A．130°

B．100°

C．80°

D．50°

已知，如图，在R t△ABC中，∠C＝90°，∠BAC的角平分线AD交BC边于D．

（1）动手操作：利用尺规作，以AB边上一点O为圆心，过A，D两点作⊙O，与AB的另一个交点为E，与AC的另一个交点为F（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由。
（2）若∠BAC=60度，CD=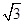，求线段BD、BE与劣弧DE所围成的图形面积．（结果保留根号和）

如图，在平面直角坐标系xOy中，⊙A与y轴相切于点B（0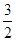，），与x轴相交于M，N两点，如果点M的坐标为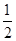（，0），求点N的坐标