初中数学圆幂定理试题

如图，AB是⊙O的直径，AC是弦，CD是⊙O的切线，C为切点，AD⊥CD于点D．

求证：（1）∠AOC=2∠ACD；（2）AC²＝AB·AD．

如图，ABCD是⊙O的内接四边形，DP∥AC，交BA的延长线于P，求证：AD·DC＝PA·BC．

已知一个圆锥的侧面展开图是一个半径为8的半圆，则该圆锥的底面半径等于_______．

用一个直径为6㎝的半圆围成一个圆锥的侧面，则这个圆锥底面圆的半径为       ㎝．

如图，在△ABC中，AB=AC，AB=8，BC=12，分别以AB、AC为直径作半圆，则图中阴影部分的面积是（   ）

A．            B．
C．            D．

若⊙A的半径是5，⊙B的半径是3，AB=2，则⊙A与⊙B的位置关系是（   ）

A．相交

B．内含

C．外切

D．内切

阅读下列材料，然后解答问题．
经过正四边形（即正方形）各顶点的圆叫做这个正四边形的外接圆，圆心是正四边形的对称中心，这个正四边形叫做这个圆的内接正四边形．
如图，正方形ABCD内接于⊙O，⊙O的面积为S₁，正方形ABCD的面积为S₂．以圆心O为顶点作∠MON，使∠MON＝90°．将∠MON绕点O旋转，OM、ON分别与⊙O交于点E、F，分别与正方形ABCD的边交于点G、H．设由OE、OF、及正方形ABCD的边围成的图形（阴影部分）的面积为S．
（1）当OM经过点A时（如图①），则S、S₁、S₂之间的关系为：            （用含S₁、S₂的代数式表示）；
（2）当OM⊥AB于G时（如图②），则（1）中的结论仍然成立吗？请说明理由；
（3）当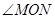旋转到任意位置时（如图③），则（1）中的结论仍然成立吗？请说明理由；

已知：如图，等边△ABC内接于⊙O，点P是劣弧上的一点（端点除外），延长BP至D，使BD=AP，连接CD．

（1）若AP过圆心O，如图①，请你判断△PDC是什么三角形？并说明理由；
（2）若AP不过圆心O，如图②，△PDC又是什么三角形？为什么？

如图所示，破残的圆形轮片上，弦AB的垂直平分线交弧AB于点C，交弦AB于点D．已知：AB=24cm，CD=8cm．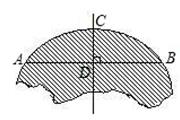

（1）求作此残片所在的圆（不写作法，保留作图痕迹）
（2）求残片所在圆的面积

每位同学都能感受到日出时美丽的景色．右图是一位同学从照片上剪切下来的画面，“图上”太阳与海平线交于A﹑B两点，他测得“图上”圆的半径为5厘米，AB=8厘米，若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟，求“图上”太阳升起的速度．

如图所示，AB是圆O的直径，以OA为直径的圆C与圆O的弦AD相交于点E．
求证：点E为AD的中点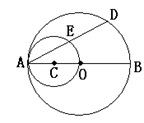

如图，AB是⊙O的直径，弦CD∥AB．若∠ABD＝65°，则∠ADC＝          °．

如图，C是以AB为直径的⊙O上一点，已知AB=5，BC=3，则圆心O到弦BC的距离是     ．

直角三角形的两边的长分别为6和8，它的外接圆的半径是__     _．

在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y=kx﹣3k+4与
⊙O交于B、C两点，则弦BC的长的最小值为（    ）

A．22              B．24              C．           D．