在数轴上,点 , 在原点 的两侧,分别表示数 ,2,将点 向右平移1个单位长度,得到点 ,若 ,则 的值为
| A. |
|
B. |
|
C. |
|
D. |
1 |
点 , 在数轴上的位置如图所示,其对应的数分别是 和 .对于以下结论:
甲:
乙:
丙:
丁:
其中正确的是

| A. |
甲乙 |
B. |
丙丁 |
C. |
甲丙 |
D. |
乙丁 |
已知数轴上有A、B、C三点,分别代表﹣24,﹣10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
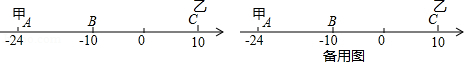
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是 .
如图,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0,O为原点.

(1)则a= ,b= ;
(2)若动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,
①当PO=2PB时,求点P的运动时间t;
②当点P运动到线段OB上时,分别取AP和OB的中点E、F,则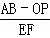 的值为 .
的值为 .
(3)有一动点Q从原点O出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动到2015次时,求点Q所对应的有理数.
如图,有一个高为5的圆柱体,现在它的底面圆周在数轴上滚动,在滚动前圆柱体底面圆周上有一点A和数轴上表示﹣1的点重合,当圆柱体滚动一周时A点恰好落在了表示2的点的位置.则这个圆柱体的侧面积是 .

在数轴上,若A点表示数﹣1,点B表示数2,A、B两点之间的距离为 .
下列几种说法中,正确的是( )
| A.0是最小的数 |
| B.任何有理数的绝对值都是正数 |
| C.最大的负有理数是﹣1 |
| D.数轴上距原点3个单位的点表示的数是±3 |
数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )

A.点A B.点B C.点C D.点D
如图,一个点从数轴上的原点开始,先向左移动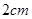 到达
到达 点,再向左移动
点,再向左移动 到达
到达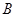 点,然后向右移动
点,然后向右移动 到达
到达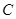 点.
点.
(1)用1个单位长度表示 ,请你在数轴上表示出
,请你在数轴上表示出 、
、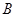 、
、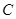 三点的位置;
三点的位置;
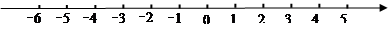
(2)把点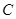 到点
到点 的距离记为
的距离记为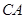 ,则
,则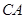 =
= 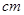 .
.
(3)阅读理解:观察式子: 因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
问题解决
若点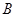 以每秒
以每秒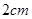 的速度向左移动,同时
的速度向左移动,同时 、
、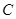 点分别以每秒
点分别以每秒 、
、 的速度向右移动.设移动时间为
的速度向右移动.设移动时间为 秒,试探索:
秒,试探索: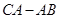 的值是否会随着
的值是否会随着 的变化而改变?请说明理由.
的变化而改变?请说明理由.
在数轴上画出表示下列各数的点,并用“<”号把它们连接起来.
点 (
( 为正整数)都在数轴上.点
为正整数)都在数轴上.点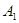 在原点
在原点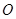 的左边,且
的左边,且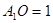 ;点
;点 在点
在点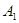 的右边,且
的右边,且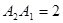 ;点
;点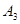 在点
在点 的左边,且
的左边,且 ;点
;点 在点
在点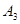 的右边,且
的右边,且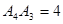 ;……,依照上述规律:
;……,依照上述规律:
(1)点 所表示的数是 ;
所表示的数是 ;
(2)点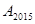 所表示的数是 .
所表示的数是 .
有理数 在数轴上的对应点的位置如图所示,则( )
在数轴上的对应点的位置如图所示,则( )

A. |
B. |
C. |
D. |
如图,先在数轴上画出表示2.5的相反数的点B,再把点A向左移动1.5个单位,得到点C,求点B,C表示的数,以及B,C两点间的距离.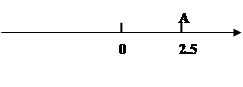
如图所示,一个点从数轴上的原点开始,先向右移动3单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图1-8并思考,完成下列各题:
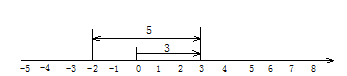
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_______,A,B两点间的距离是________;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是_______,A,B两点间的距离为________;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_________,A,B两点间的距离是________.
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么,请你猜想终点B表示什么数?A,B两点间的距离为多少?