如图所示,空间分布着有理想边界的匀强电场和匀强磁场。左侧匀强电场的场强大小为E、方向水平向右,电场宽度为L;中间区域及右侧匀强磁场的磁感应强度大小均为B,方向垂直纸面向外和向里。一个质量为m、电量为q、不计重力的带正电的粒子从电场的左边缘的O点由静止开始运动,穿过中间磁场区域进入右侧磁场区域后,又回到O点,然后重复上述运动过程。要求:
定性画出粒子运动轨迹,并求出粒子在磁场中运动的轨道半径R;
中间磁场区域的宽度d;
带电粒子从O点开始运动到第一次回到O点所用时间t。
长为L,间距也为L的两平行金属板间有垂直向里的匀强磁场,如图所示,磁感应强度为B,今有质量为m、带电量为q的正离子从平行板左端中点以平行于金属板的方向射入磁场。欲使离子不打在极板上,入射离子的速度大小应满足的条件是[ ]
① ②
②
③  ④
④
| A.①② | B.①③ | C.②③ | D.②④ |
如图所示,分布在半径为 的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里。电荷量为
的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里。电荷量为 、质量为
、质量为 的带正电粒子从磁场边缘
的带正电粒子从磁场边缘 点处沿圆的半径
点处沿圆的半径 O方向射入磁场,离开磁场时速度方向偏转了
O方向射入磁场,离开磁场时速度方向偏转了 角,试求:
角,试求:
粒子做圆周运动的半径R;
粒子的入射速度
 ;
;若保持粒子的速率不变,从
 点入射时速度的方向顺时针转过
点入射时速度的方向顺时针转过 角,粒子在磁场中运动的时间
角,粒子在磁场中运动的时间 。
。
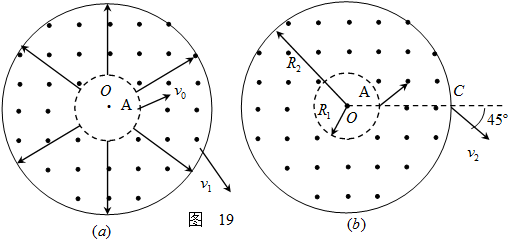
如图(a)所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在辐射状电场和垂直纸面的匀强磁场,内外圆间的电势差U为常量,R1=R0,R2=3R0,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力。已知粒子从外圆上以速度v1射出,求粒子在A点的初速度v0的大小。
若撤去电场,如图19(b),已知粒子从OA延长线与外圆的交点C以速度v2射出,方向与OA延长线成45°角,求磁感应强度的大小及粒子在磁场中运动的时间。
在图(b)中,若粒子从A点进入磁场,速度大小为v3,方向不确定,要使粒子一定能够从外圆射出,磁感应强度应小于多少?
如图所示,在x轴上方及下方存在方向垂直纸面向里的匀强磁场,上方磁场的磁感应强度大小为B、下方磁场的磁感应强度大小为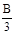 。一质量为m、电量为q的带正电粒子从x轴上O点以速度v0垂直x轴向上射出。不计粒子重力。
。一质量为m、电量为q的带正电粒子从x轴上O点以速度v0垂直x轴向上射出。不计粒子重力。
求: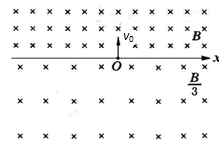
射出后粒子第二次到达x轴时离O点的距离, 并画出该过程粒子运动的轨迹;
射出后粒子经过多长时间第二次到达x轴。
如图所示,边界MN上方存在区域足够大、方向垂直纸面向里的匀强磁场。有两个质量和电荷量均相同的正、负离子,从O点以相同的速率射入磁场中,射入方向与边界成θ=600角。若不计重力。则
| A.正离子在磁场中运动时间是负离子的2倍 |
| B.负离子在磁场中运动时间是正离子的2倍 |
| C.正离子、负离子在磁场中运动时间相等 |
| D.正负离子在磁场中运动轨道半径相等 |
正方形区域ABCD中有垂直于纸面向里的匀强磁场,一个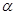 粒子(不计重力)以一定速度从AB边的中点M沿既垂直于AB边又垂直于磁场的方向射入磁场,正好从AD边的中点N射出。若将磁感应强度B变为原来的2倍,其他条件不变,则这个
粒子(不计重力)以一定速度从AB边的中点M沿既垂直于AB边又垂直于磁场的方向射入磁场,正好从AD边的中点N射出。若将磁感应强度B变为原来的2倍,其他条件不变,则这个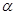 粒子射出磁场的位置是( )
粒子射出磁场的位置是( )
| A.A点 | B.ND之间的某一点 |
| C.CD之间的某一点 | D.BC之间的某一点 |
在光滑绝缘的水平面(纸面)上建有如图所示的平面直角坐标系,在此水平面上可视为质点的不带电小球a静止于坐标系的原点O,可视为质点的带正电小球b静止在坐标为(0,-h)的位置上。现加一方向沿y轴正方向、电场强度大小为E、范围足够大的匀强电场,同时给a球以某一速度使其沿x轴正方向运动。当b球到达坐标系原点O时速度为v0,此时立即撤去电场而改加一方向垂直于纸面向外、磁感应强度大小为B、范围足够大的匀强磁场,最终b球能与a球相遇。求:b
 球的比荷
球的比荷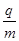 ;
;从b球到达原点O开始至b球与a球相遇所需的时间;
撤去电场时,a球的位置坐标。
如图所示,A、B是竖直放置的平行板电容器,B板中央有一个小孔,恰好跟一个边界是等边三角形的一个匀强磁场的顶端相接,磁场方向垂直纸面向里,磁感应强度为B,其中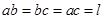 ,磁场的
,磁场的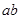 边界平行于平行板A和B。
边界平行于平行板A和B。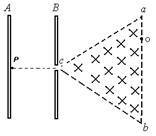
若在A板上正对B板小孔的P处,静止释放一个带电量为
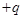 、质量为
、质量为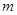 的带电粒子(重力不计),恰能从图中O点射出,且
的带电粒子(重力不计),恰能从图中O点射出,且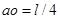 ,则A、B两板间的电压
,则A、B两板间的电压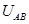 是多少?
是多少?若要上述带电粒子在磁场中的运动时间与平行板A、B间的电压无关,则A、B两板间的电压
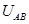 又是多少?
又是多少?
如图所示,在边长为L的正方形ABCD 区域内存在方向垂直纸面向外的匀强磁场.一带电粒子(重力不计)以速度v 沿AB 边方向射人磁场,之后粒子恰好从CD 边的中点E 射出,则
| A.该粒子一定带负电 |
| B.该粒子在磁场中做圆周运动的轨道半径为L/2 |
| C.若该粒子射人磁场的速度大小为2v,方向不变,则粒子将从BC 边的中点F 射出 |
| D.若该粒子射人磁场的速度大小为2v,方向不变,则粒子在磁场中的运动时间是原来的1/2 |
如图甲所示的坐标系中,第四限象内存在垂直于纸面向里的有界匀强磁场, 方向的宽度OA=20
方向的宽度OA=20 cm,
cm, 方向无限制,磁感应强度B0=1×10-4T。现有一比荷为q/m=2×1011C/kg的正离子以某一速度从O点射入磁场,α=60°,离子通过磁场后刚好从A点射出。
方向无限制,磁感应强度B0=1×10-4T。现有一比荷为q/m=2×1011C/kg的正离子以某一速度从O点射入磁场,α=60°,离子通过磁场后刚好从A点射出。
求离子进入磁场B0的速度的大小;
离子进入磁场B0后,某时刻再加一个同方向的匀强磁场,使离子做完整的圆周运动,求所加磁场磁感应强度的最小值;
离子进入磁场B0后,再加一个如图乙所示的变化磁场(正方向与B0方向相同,不考虑磁场变化所产生的电场),求离子从O点到A点的总时间。
如图所示,质量为m,电荷量为e的电子从坐标原点O处沿xOy平面射入第一象限内,射入时的速度方向不同,但大小均为v0.现在某一区域内加一方向向外且垂直于xOy平面的匀强磁场,磁感应强度大小为B,若这些电子穿过磁场后都能垂直地射到与y轴平行的荧光屏MN上,求:
电子从y轴穿过的范围;
荧光屏上光斑的长度;
所加磁场范围的最小面积.
如图所示,直角三角形ABC中存在一匀强磁场,比荷相同的两个粒子沿AB方向自A点射入磁场,分别从AC边上的P、Q两点射出,则 
| A.从P射出的粒子速度大 |
| B.从Q射出的粒子速度大 |
| C.从P射出的粒子,在磁场中运动的时间长 |
| D.两粒子在磁场中运动的时间一样长 |
利用如图所示装置可以选择一定速度范围内的带电粒子.图中板MN上方是磁感应强度大小为B、方向垂直纸面向里的匀强磁场,板上有两条宽度分别为2d和d的缝,两缝近端相距为L.一群质量为m、电荷量为q,具有不同速度的粒子从宽度为2d的缝垂直于板MN进入磁场,对于能够从宽度为d的缝射出的粒子,下列说法正确的是
A.粒子带正电
B.射出粒子的最大速度为
C.保持d和L不变,增大B,射出粒子的最大速度与最小速度之差增大
D.保持d和B不变,增大L,射出粒子的最大速度与最小速度之差不变