如果将点 绕定点 旋转 后与点 重合,那么称点 与点 关于点 对称,定点 叫对称中心,此时,点 是线段 的中点,如图,在直角坐标系中, 的顶点 的坐标分别为 ,点列 中的相邻两点都关于 的一个顶点对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,…,对称中心分别是 ,且这些对称中心依次循环,已知 的坐标为 ,试写出 的坐标.
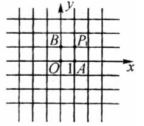
如果将点 绕定点 旋转 后与点 重合,那么称点 与点 关于点 对称,定点 叫对称中心,此时,点 是线段 的中点,如图,在直角坐标系中, 的顶点 的坐标分别为 ,点列 中的相邻两点都关于 的一个顶点对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,…,对称中心分别是 ,且这些对称中心依次循环,已知 的坐标为 ,试写出 的坐标.
