已知二次函数
.
(1)若
,且该二次函数的图象过点
,求c的值;
(2)如图所示,在平面直角坐标系xOy中,该二次函数的图象与x轴相交于不同的两点
、
,其中
、
,且该二次函数的图象的顶点在矩形
的边
上,其对称轴与
轴、
分别交于点
与
轴相交于点
,且满足
.
①求关于
的一元二次方程
的根的判别式的值;
②若
,令
,求
的最小值.
阅读材料:十六世纪的法国数学家弗朗索瓦•韦达发现了一元二次方程的根与系数之间的关系,可表述为“当判别式
时,关于
的一元二次方程
的两个根
有如下关系:
,
”.此关系通常被称为“韦达定理”.



 C.
C.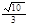 D. 2
D. 2
 秒, ∠APB的度数为y度,则下列图象中表示y与t之间函数关系最恰当的是( )
秒, ∠APB的度数为y度,则下列图象中表示y与t之间函数关系最恰当的是( )

 ,乙组方差
,乙组方差 ,则乙组数比甲组数稳定
,则乙组数比甲组数稳定
 粤公网安备 44130202000953号
粤公网安备 44130202000953号