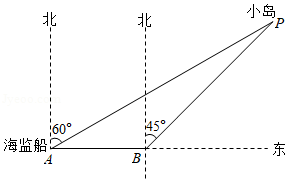
某海域有一小岛 ,在以 为圆心,半径 为 海里的圆形海域内有暗礁.一海监船自西向东航行,它在 处测得小岛 位于北偏东 的方向上,当海监船行驶 海里后到达 处,此时观测小岛 位于 处北偏东 方向上.
(1)求 , 之间的距离 ;
(2)若海监船由 处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由 处开始沿南偏东至多多少度的方向航行能安全通过这一海域?
相关知识点
推荐套卷
某海域有一小岛 ,在以 为圆心,半径 为 海里的圆形海域内有暗礁.一海监船自西向东航行,它在 处测得小岛 位于北偏东 的方向上,当海监船行驶 海里后到达 处,此时观测小岛 位于 处北偏东 方向上.
(1)求 , 之间的距离 ;
(2)若海监船由 处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由 处开始沿南偏东至多多少度的方向航行能安全通过这一海域?
