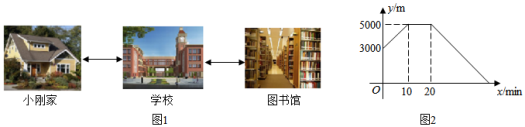
如图1,小刚家、学校、图书馆在同一条直线上,小刚骑自行车匀速从学校到图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离 与他所用的时间 的函数关系如图2所示.
(1)小刚家与学校的距离为 ,小刚骑自行车的速度为 ;
(2)求小刚从图书馆返回家的过程中, 与 的函数表达式;
(3)小刚出发35分钟时,他离家有多远?
相关知识点
推荐套卷
如图1,小刚家、学校、图书馆在同一条直线上,小刚骑自行车匀速从学校到图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离 与他所用的时间 的函数关系如图2所示.
(1)小刚家与学校的距离为 ,小刚骑自行车的速度为 ;
(2)求小刚从图书馆返回家的过程中, 与 的函数表达式;
(3)小刚出发35分钟时,他离家有多远?
