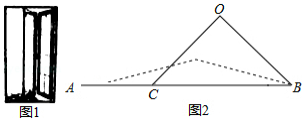
图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框上,通过推动左侧活页门开关.图2是其俯视简化示意图,已知轨道 ,两扇活页门的宽 ,点 固定,当点 在 上左右运动时, 与 的长度不变.(所有的结果保留小数点后一位)
(1)若 ,求 的长;
(2)当点 从点 向右运动 时,求点 在此过程中运动的路径长.
参考数据: . , , 取3.14.
相关知识点
推荐套卷
图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框上,通过推动左侧活页门开关.图2是其俯视简化示意图,已知轨道 ,两扇活页门的宽 ,点 固定,当点 在 上左右运动时, 与 的长度不变.(所有的结果保留小数点后一位)
(1)若 ,求 的长;
(2)当点 从点 向右运动 时,求点 在此过程中运动的路径长.
参考数据: . , , 取3.14.
