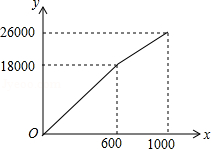
为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为 的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为 ,种草所需费用 (元)与 的函数关系式为 ,其图象如图所示:栽花所需费用 (元 与 的函数关系式为 .
(1)请直接写出 、 和 的值;
(2)设这块 空地的绿化总费用为 (元),请利用 与 的函数关系式,求出绿化总费用 的最大值;
(3)若种草部分的面积不少于 ,栽花部分的面积不少于 ,请求出绿化总费用 的最小值.
相关知识点
推荐套卷
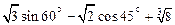 ;②
;②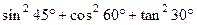
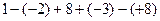 (2)
(2)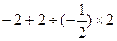
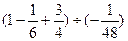 (4)
(4)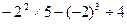
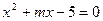 的一个根,求m的值及方程的另一根x2
的一个根,求m的值及方程的另一根x2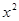 -3x-2=0
-3x-2=0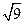 +|-2|+
+|-2|+ +(-1)2011(2)
+(-1)2011(2)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号