抛物线 经过点 和点 ．
（1）求该抛物线所对应的函数解析式；
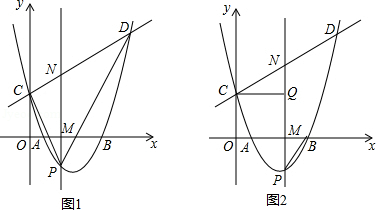
（2）该抛物线与直线 相交于 、 两点，点 是抛物线上的动点且位于 轴下方，直线 轴，分别与 轴和直线 交于点 、 ．
①连接 、 ，如图1，在点 运动过程中， 的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；
②连接 ，过点 作 ，垂足为点 ，如图2，是否存在点 ，使得 与 相似？若存在，求出满足条件的点 的坐标；若不存在，说明理由．
如图，⊙O的半径为1，点P是⊙O上一点，弦AB垂直平分线段OP，点D是
上任一点（与端点A、B不重合），DE⊥AB于点E，以点D为圆心、DE长为半径作⊙D，分别过点A、B作⊙D的切线，两条切线相交于点C．
（1）求弦AB的长；
（2）判断∠ACB是否为定值，若是，求出∠ACB的大小；否则，请说明理由；
（3）记△ABC的面积为S，若
＝4
，求△ABC的周长.
)0+(
)-1-
-|-1|取12.4g碳酸铜（CuCO3，式量124）粉末放入盛有92g稀硫酸的烧杯中，恰好完全反应，生产的CO2气体全部逸出。请计算：
（1）反应生产H2O的质量。
（2）反应后烧杯中硫酸铜（式量160）溶液溶质的质量分数。
某部分变质的NaOH试剂经处理后只含有NaOH和Na2CO3两种物质。小明同学从中均匀取出9.3g样品用19.9g水溶解后，再向其中缓慢滴加10%的稀盐酸至恰好完全反应时，用去稀盐酸73g，经测定共放出气体2.2g。
（1）向样品中加入稀盐酸至恰好完全反应时，发生的两个反应可用化学方程式表示为：
_______________________________________，_______________________________________；
9.3g样品中，含Na2CO3的质量为_____________g，含NaOH的质量为_____________g。
（2）通过计算确定原NaOH试剂的变质程度。（用质量百分数表示）
（3）上述恰好完全反应后的溶液中，溶质的质量分数是多少？（用百分数表示，保留一位小数）
经过A（
，0）、C（0，
）两点，与
轴交于另一点B。
，
）在第四象限的抛物线上，求点D关于直线BC对称的点
，的坐标。
，若存在，请求出P点的坐标；若不存在，请说明理由
粤公网安备 44130202000953号