《九章算术》是中国传统数学最重要的著作，在“勾股”章中有这样一个问题：“今有邑方二百步，各中开门，出东门十五步有木，问：出南门几步而见木？”
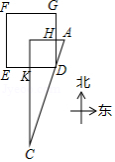
用今天的话说，大意是：如图， 是一座边长为200步 “步”是古代的长度单位）的正方形小城，东门 位于 的中点，南门 位于 的中点，出东门15步的 处有一树木，求出南门多少步恰好看到位于 处的树木（即点 在直线 上）？请你计算 的长为 步．
=
，则
。
与
是同类项，则m＋n＝。相关知识点
推荐套卷
《九章算术》是中国传统数学最重要的著作，在“勾股”章中有这样一个问题：“今有邑方二百步，各中开门，出东门十五步有木，问：出南门几步而见木？”
用今天的话说，大意是：如图， 是一座边长为200步 “步”是古代的长度单位）的正方形小城，东门 位于 的中点，南门 位于 的中点，出东门15步的 处有一树木，求出南门多少步恰好看到位于 处的树木（即点 在直线 上）？请你计算 的长为 步．
粤公网安备 44130202000953号