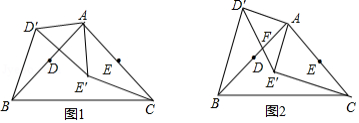
已知 中, , , 、 分别是 、 的中点, 将 绕点 按顺时针方向旋转一个角度 得到△ ,连接 、 ,如图 1 .
(1) 求证: ;
(2) 如图 2 ,当 时, 设 与 交于点 ,求 的值 .
相关知识点
推荐套卷
已知 中, , , 、 分别是 、 的中点, 将 绕点 按顺时针方向旋转一个角度 得到△ ,连接 、 ,如图 1 .
(1) 求证: ;
(2) 如图 2 ,当 时, 设 与 交于点 ,求 的值 .
