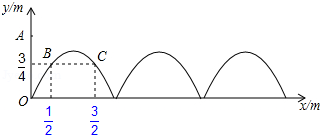
如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用 表示.已知抛物线上 , 两点到地面的距离均为 ,到墙边 的距离分别为 , .
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为 ,则最多可以连续绘制几个这样的拋物线型图案?
相关知识点
推荐套卷
如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用 表示.已知抛物线上 , 两点到地面的距离均为 ,到墙边 的距离分别为 , .
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为 ,则最多可以连续绘制几个这样的拋物线型图案?
