平面直角坐标系 中,点 、 的横坐标分别为 、 ,二次函数 的图象经过点 、 ,且 、 满足 为常数).
(1)若一次函数 的图象经过 、 两点.
①当 、 时,求 的值;
②若 随 的增大而减小,求 的取值范围;
(2)当 且 、 时,判断直线 与 轴的位置关系,并说明理由;
(3)点 、 的位置随着 的变化而变化,设点 、 运动的路线与 轴分别相交于点 、 ,线段 的长度会发生变化吗?如果不变,求出 的长;如果变化,请说明理由.
相关知识点
推荐套卷
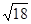 -4
-4 +
+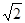

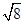 +(
+(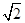 -1)+(
-1)+(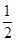 )0.
)0.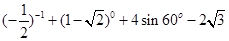
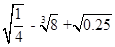
 粤公网安备 44130202000953号
粤公网安备 44130202000953号