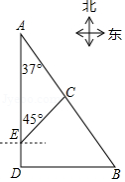
如图,港口 位于港口 的南偏东 方向,灯塔 恰好在 的中点处.一艘海轮位于港口 的正南方向,港口 的正西方向的 处,它沿正北方向航行 到达 处,测得灯塔 在北偏东 方向上,这时, 处距离港口 有多远?(参考数据: , ,
相关知识点
推荐套卷
如图,港口 位于港口 的南偏东 方向,灯塔 恰好在 的中点处.一艘海轮位于港口 的正南方向,港口 的正西方向的 处,它沿正北方向航行 到达 处,测得灯塔 在北偏东 方向上,这时, 处距离港口 有多远?(参考数据: , ,
