如图1,已知一次函数 的图象与 轴、 轴分别交于 、 两点,抛物线 过 、 两点,且与 轴交于另一点 .
(1)求 、 的值;
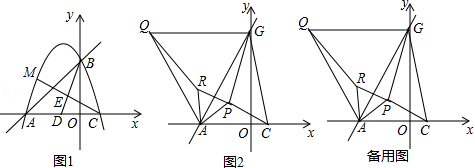
(2)如图1,点 为 的中点,点 在线段 上,且 ,连接 并延长交抛物线于点 ,求点 的坐标;
(3)将直线 绕点 按逆时针方向旋转 后交 轴于点 ,连接 ,如图2, 为 内一点,连接 、 、 ,分别以 、 为边,在他们的左侧作等边 ,等边 ,连接
①求证: ;
②求 的最小值,并求出当 取得最小值时点 的坐标.
相关知识点
推荐套卷
 粤公网安备 44130202000953号
粤公网安备 44130202000953号