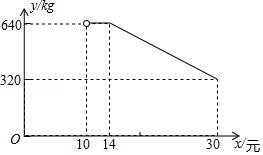
网络销售是一种重要的销售方式．某乡镇农贸公司新开设了一家网店，销售当地农产品．其中一种当地特产在网上试销售，其成本为每千克10元．公司在试销售期间，调查发现，每天销售量 与销售单价 （元 满足如图所示的函数关系（其中 ．
（1）直接写出 与 之间的函数关系式及自变量的取值范围．
（2）若农贸公司每天销售该特产的利润要达到3100元，则销售单价 应定为多少元？
（3）设每天销售该特产的利润为 元，若 ，求：销售单价 为多少元时，每天的销售利润最大？最大利润是多少元？
相关试题
某书店老板去图书批发市场购买某种图书．第一次用1200元购书若干本，并按该书定价7元出售，很快售完．由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了20%，他用1500元所购该书数量比第一次多10本．当按定价售出200本时，出现滞销，便以定价的4折售完剩余的书．试问该老板这两次售书总体上是赔钱了，还是赚钱了（不考虑其它因素）？若赔钱，赔多少？若赚钱，赚多少？
在不透明的口袋中，有四只形状、大小、质地完全相同的小球，四只小球上分别标有数字，2，4，- . 小明先从盒子里随机取出一只小球(不放回)，记下数字作为平面直角坐标系内点的横坐标；再由小华随机取出一只小球，记下数字作为平面直角坐标系内点的纵坐标.用列表法或画树状图，表示所有这些点的坐标；
小刚为小明、小华两人设计了一个游戏：当上述（1）中的点在第一象限时小明获胜，否则小华获胜. 你认为这个游戏公平吗？请说明理由.
某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下面是水平放置的破裂管道有水部分的截面．若这个输水管道有水部分的水面宽
，水面最深地方的高度为4cm，求这个圆形截面的半径．
，并把解集在数轴上表示出来．相关知识点
推荐套卷
粤公网安备 44130202000953号