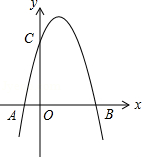
如图，二次函数 的图象与 轴的一个交点为 ，另一个交点为 ，且与 轴相交于 点．
（1）求 的值及 点坐标；
（2）在直线 上方的抛物线上是否存在一点 ，使得它与 ， 两点构成的三角形面积最大，若存在，求出此时 点坐标；若不存在，请简要说明理由；
（3） 为抛物线上一点，它关于直线 的对称点为
①当四边形 为菱形时，求点 的坐标；
②点 的横坐标为 ，当 为何值时，四边形 的面积最大，请说明理由．
相关试题
. 汶川地震后，抢险队派一架直升飞机去A、B两个村庄抢险，飞机在距地面450米上空的P点，测得A村的俯角为
，B村的俯角为
．（如图）．求A、B两个村庄间的距离．（结果精确到米，参考数据
）
，sin∠BCE=
. 求CE的长.
已知二次函数
的图象如图所示，它与x轴的一个交点的坐标为（－1，0），与y轴的交点坐标为（0，－3）．
（1）求此二次函数的解析式；
（2）求此二次函数的图象与x轴的另一个交点的坐标；
（3）根据图象回答：当x取何值时，y＜0？
的图象经过点（1，0）和（-5，0）两点，顶点纵坐标为
，求这个二次函数的解析式。
相关知识点
推荐套卷
粤公网安备 44130202000953号