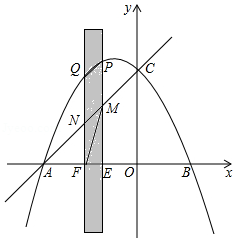
如图，抛物线与 轴交于点 和点 ．与 轴交于点 ．有一宽度为1，长度足够的矩形（阴影部分）沿 轴方向平移，与 轴平行的一组对边交抛物线于点 和 ，交直线 于点 和 ．交 轴于点 和 ．
（1）求抛物线的解析式；
（2）当点 和 都在线段 上时，连接 ，如果 ，求点 的坐标；
（3）在矩形的平移过程中，当以点 ， ， ， 为顶点的四边形是平行四边形时，求点 的坐标．
在平面直角坐标系 中，已知抛物线 经过 两点． 是抛物线上一点，且在直线 的上方．
（1）求抛物线的解析式；
（2）若 面积是 面积的2倍，求点 的坐标；
（3）如图， 交 于点 ， 交 于点 ．记 ， , 的面积分别为 ．判断 是否存在最大值．若存在，求出最大值；若不存在，请说明理由．
已知 ， ， ．
（1）如图1， 平分 ，求证：四边形 是菱形；
（2）如图2，将（1）中的 绕点 逆时针旋转（旋转角小于 ）， 的延长线相交于点 ，用等式表示 与 之间的数量关系，并证明；
（3）如图3，将（1）中的 绕点 顺时针旋转（旋转角小于 ），若 ，求 的度数．
如图，BD是矩形ABCD的对角线．
（1）求作 ，使得 与 相切（要求：尺规作图，不写作法，保留作图痕迹）；
（2）在（1）的条件下，设BD与 相切于点E， ，垂足为F．若直线CF与 相切于点G，求 的值．
在学校开展“劳动创造美好生活”主题系列活动中，八年级（1）班负责校园某绿化角的设计、种植与养护．同学们约定每人养护一盆绿植，计划购买绿萝和吊兰两种绿植共46盆，且绿萝盆数不少于吊兰盆数的2倍．已知绿萝每盆9元，吊兰每盆6元．
（1）采购组计划将预算经费390元全部用于购买绿萝和吊兰，问可购买绿萝和吊兰各多少盆？
（2）规划组认为有比390元更省钱的购买方案，请求出购买两种绿植总费用的最小值．
粤公网安备 44130202000953号