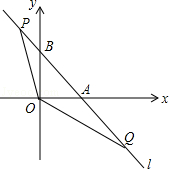
如图,直线 与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限, .
(1)求△AOB的周长;
(2)设 ,试用含t的代数式表示点P的坐标;
(3)当动点P,Q在直线l上运动到使得△AOQ与△BPO的周长相等时,记 ,若过点A的二次函数 同时满足以下两个条件:
① ;
②当 时,函数y的最大值等于 ,求二次项系数a的值.
相关知识点
推荐套卷
如图,直线 与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限, .
(1)求△AOB的周长;
(2)设 ,试用含t的代数式表示点P的坐标;
(3)当动点P,Q在直线l上运动到使得△AOQ与△BPO的周长相等时,记 ,若过点A的二次函数 同时满足以下两个条件:
① ;
②当 时,函数y的最大值等于 ,求二次项系数a的值.
