科技馆是少年儿童节假日游玩的乐园．
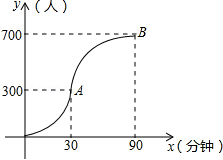
如图所示，图中点的横坐标x表示科技馆从8：30开门后经过的时间（分钟），纵坐标y表示到达科技馆的总人数．图中曲线对应的函数解析式为 ，10：00之后来的游客较少可忽略不计．
（1）请写出图中曲线对应的函数解析式；
（2）为保证科技馆内游客的游玩质量，馆内人数不超过684人，后来的人在馆外休息区等待．从10：30开始到12：00馆内陆续有人离馆，平均每分钟离馆4人，直到馆内人数减少到624人时，馆外等待的游客可全部进入．请问馆外游客最多等待多少分钟？
相关试题
平移后经过点
，
，求平移后的抛物线的表达式．
是一元二次方程
的实数根，求代数式
的值．
对于正整数
，定义
，其中
表示的首位数字、末位数字的平方和．例如：
，
．
规定
，
（
为正整数）．例如：
，
．
（1）求：
____________，
______________；
（2）若
，则正整数m的最小值是_____________．
中，已知点D（0，4），E（0，1）．
，那么点F对线段DE的视角∠DFE为_________度；
相关知识点
推荐套卷
粤公网安备 44130202000953号