下列说法中正确的有( )
① 的算术平方根是6
②关于 x的方程 mx 2+2 x+1=0有实数根,那么 m的取值范围是 m≤1且 m≠0.
③一组数据:1,0,2,1,0,2的方差是 .
④已知直角三角形的两边长分别为3和4,则第三边的长为5.
⑤在平行四边形、线段、角、等边三角形四个图形中,既是轴对称图形又是中心对称图的只有一个.
| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
相关知识点
推荐套卷
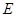 ,
,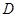 ,
, ,
,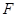 在同一条直线上。若
在同一条直线上。若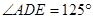 ,则
,则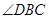 的度数为
的度数为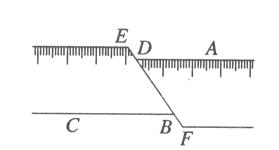
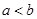 ,则下列不等式中成立的是
,则下列不等式中成立的是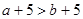
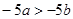

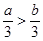
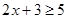 的解集在数轴上表示正确的是
的解集在数轴上表示正确的是 粤公网安备 44130202000953号
粤公网安备 44130202000953号