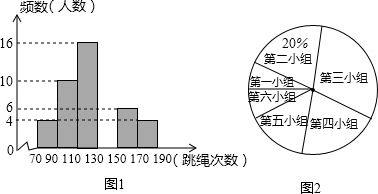
在大课间活动中，同学们积极参加体育锻炼，小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试，并以测试数据为样本绘制如图所示的部分频数分布直方图（从左到右依次分为六个小组，每小组含最小值，不含最大值）和扇形统计图，若“一分钟跳绳”次数不低于130次的成绩为优秀，全校共有1200名学生，根据图中提供的信息，估计该校学生“一分钟跳绳”成绩优秀的人数为 人．
相关试题
，则
▲ ．
的结果是 ▲ ．
，则DE=_________．
相关知识点
推荐套卷
在大课间活动中，同学们积极参加体育锻炼，小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试，并以测试数据为样本绘制如图所示的部分频数分布直方图（从左到右依次分为六个小组，每小组含最小值，不含最大值）和扇形统计图，若“一分钟跳绳”次数不低于130次的成绩为优秀，全校共有1200名学生，根据图中提供的信息，估计该校学生“一分钟跳绳”成绩优秀的人数为 人．
粤公网安备 44130202000953号