某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元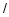 件的商品售后,经过统计得到此商品单价在第
件的商品售后,经过统计得到此商品单价在第 天
天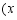 为正整数)销售的相关信息,如表所示:
为正整数)销售的相关信息,如表所示:
销售量 |
|
销售单价 |
当 |
当 |
(1)请计算第几天该商品单价为25元 件?
件?
(2)求网店销售该商品30天里所获利润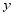 (元
(元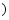 关于
关于 (天
(天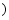 的函数关系式;
的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
相关知识点
推荐套卷
某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元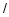 件的商品售后,经过统计得到此商品单价在第
件的商品售后,经过统计得到此商品单价在第 天
天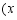 为正整数)销售的相关信息,如表所示:
为正整数)销售的相关信息,如表所示:
销售量 |
|
销售单价 |
当 |
当 |
(1)请计算第几天该商品单价为25元 件?
件?
(2)求网店销售该商品30天里所获利润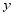 (元
(元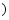 关于
关于 (天
(天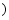 的函数关系式;
的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?