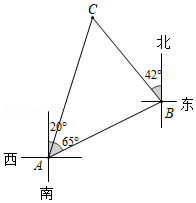
如图,一艘船由 港沿北偏东 方向航行 到 港,然后再沿北偏西 方向航行至 港,已知 港在 港北偏东 方向.
(1)直接写出 的度数;
(2)求 、 两港之间的距离.(结果用含非特殊角的三角函数及根式表示即可)
相关知识点
推荐套卷
如图,一艘船由 港沿北偏东 方向航行 到 港,然后再沿北偏西 方向航行至 港,已知 港在 港北偏东 方向.
(1)直接写出 的度数;
(2)求 、 两港之间的距离.(结果用含非特殊角的三角函数及根式表示即可)
