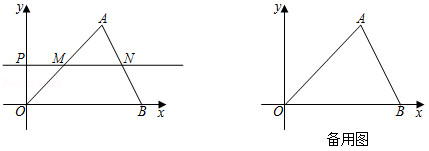如图,在平面直角坐标系中, 的顶点 是坐标原点,点 的坐标为 ,点 的坐标为 ,动点 从 开始以每秒1个单位长度的速度沿 轴正方向运动,设运动的时间为 秒 ,过点 作 轴,分别交 , 于点 , .
(1)填空: 的长为 , 的长为 ;
(2)当 时,求点 的坐标;
(3)请直接写出 的长为 (用含 的代数式表示);
(4)点 是线段 上一动点(点 不与点 , 重合), 和 的面积分别表示为 和 ,当 时,请直接写出 (即 与 的积)的最大值为 .
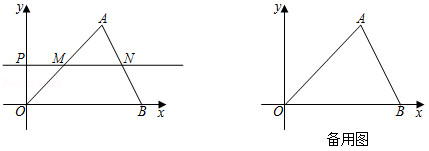
推荐套卷
如图,在平面直角坐标系中, 的顶点 是坐标原点,点 的坐标为 ,点 的坐标为 ,动点 从 开始以每秒1个单位长度的速度沿 轴正方向运动,设运动的时间为 秒 ,过点 作 轴,分别交 , 于点 , .
(1)填空: 的长为 , 的长为 ;
(2)当 时,求点 的坐标;
(3)请直接写出 的长为 (用含 的代数式表示);
(4)点 是线段 上一动点(点 不与点 , 重合), 和 的面积分别表示为 和 ,当 时,请直接写出 (即 与 的积)的最大值为 .