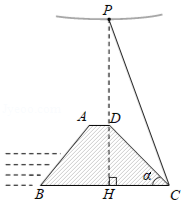
沿江大堤经过改造后的某处横断面为如图所示的梯形 ,高 米,斜坡 的坡度 .此处大堤的正上方有高压电线穿过, 表示高压线上的点与堤面 的最近距离 、 、 在同一直线上),在点 处测得 .
(1)求斜坡 的坡角 ;
(2)电力部门要求此处高压线离堤面 的安全距离不低于18米,请问此次改造是否符合电力部门的安全要求?
(参考数据: , , ,
相关知识点
推荐套卷
沿江大堤经过改造后的某处横断面为如图所示的梯形 ,高 米,斜坡 的坡度 .此处大堤的正上方有高压电线穿过, 表示高压线上的点与堤面 的最近距离 、 、 在同一直线上),在点 处测得 .
(1)求斜坡 的坡角 ;
(2)电力部门要求此处高压线离堤面 的安全距离不低于18米,请问此次改造是否符合电力部门的安全要求?
(参考数据: , , ,
