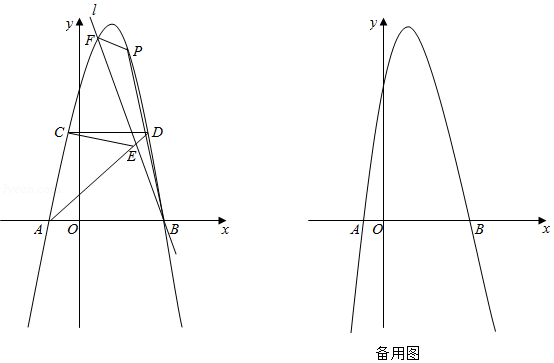
如图,抛物线与轴交于,两点在的右侧),且经过点和点.
(1)求抛物线的函数表达式;
(2)连接,经过点的直线与线段交于点,与抛物线交于另一点.连接,,,的面积与的面积之比为,点为直线上方抛物线上的一个动点,设点的横坐标为.当为何值时,的面积最大?并求出最大值;
(3)在抛物线上,当时,的取值范围是,求的取值范围.(直接写出结果即可)
相关知识点
推荐套卷
如图,抛物线与轴交于,两点在的右侧),且经过点和点.
(1)求抛物线的函数表达式;
(2)连接,经过点的直线与线段交于点,与抛物线交于另一点.连接,,,的面积与的面积之比为,点为直线上方抛物线上的一个动点,设点的横坐标为.当为何值时,的面积最大?并求出最大值;
(3)在抛物线上,当时,的取值范围是,求的取值范围.(直接写出结果即可)
