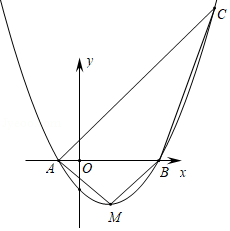
如图,已知抛物线经过点、.
(1)求抛物线的解析式,并写出顶点的坐标;
(2)若点在抛物线上,且点的横坐标为8,求四边形的面积;
(3)定点在轴上,若将抛物线的图象向左平移2个单位,再向上平移3个单位得到一条新的抛物线,点在新的抛物线上运动,求定点与动点之间距离的最小值(用含的代数式表示)
相关知识点
推荐套卷
如图,已知抛物线经过点、.
(1)求抛物线的解析式,并写出顶点的坐标;
(2)若点在抛物线上,且点的横坐标为8,求四边形的面积;
(3)定点在轴上,若将抛物线的图象向左平移2个单位,再向上平移3个单位得到一条新的抛物线,点在新的抛物线上运动,求定点与动点之间距离的最小值(用含的代数式表示)
