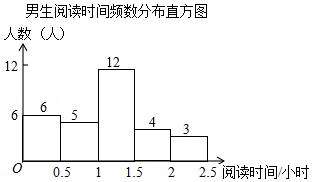
某校为了解学生课外阅读情况，就学生每周阅读时间随机调查了部分学生，调查结果按性别整理如下：
女生阅读时间人数统计表
阅读时间（小时） |
人数 |
占女生人数百分比 |
4 |
||
5 |
||
6 |
||
2 |
根据图表解答下列问题：
（1）在女生阅读时间人数统计表中， ， ；
（2）此次抽样调查中，共抽取了 名学生，学生阅读时间的中位数在 时间段；
（3）从阅读时间在小时的5名学生中随机抽取2名学生参加市级阅读活动，恰好抽到男女生各一名的概率是多少？
如图，将△ABC在网格中（网格中每个小正方形的边长均为1）依次进行位似变换、轴对称变换和平移变换后得到△A1B1C1．
（1）△ABC与△A1B1C1的位似比等于 ；
（2）在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2；
（3）请写出△A1B1C1是由△A2B2C2怎样平移得到的？
（4）设点P（x，y）为△ABC内一点，依次经过上述三次变换后，点P的对应点的坐标为 ．
如图，已知经过点D（2，
）的抛物线
（m为常数，且m＞0）与x轴交于点A、B（点A位于B的左侧），与y轴交于点C．
（1）填空：m的值为 ，点A的坐标为 ；
（2）根据下列描述，用尺规完成作图（保留作图痕迹，不写作法）：连接AD，在x轴上方作射线AE，使∠BAE=∠BAD，过点D作x轴的垂线交射线AE于点E；
（3）动点M、N分别在射线AB、AE上，求ME+MN的最小值；
（4）t是过点A平行于y轴的直线，P是抛物线上一点，过点P作l的垂线，垂足为点G，请你探究：是否存在点P，使以P、G、A为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，说明理由．
（·辽宁锦州）如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C，D不重合）．
（1）如图①，当α=90°时，DE，DF，AD之间满足的数量关系是 ；
（2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF=
AD，请给出证明；
（3）在（2）的条件下，若旋转过程中∠QPN的边PQ与射线AD交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．
（·辽宁锦州）如图，在平面直角坐标系中，线段AB的两个端点是A（﹣5，1），B（﹣2，3），线段CD的两个端点是C（﹣5，﹣1），D（﹣2，﹣3）．
（1）线段AB与线段CD关于直线对称，则对称轴是 ；
（2）平移线段AB得到线段A1B1，若点A的对应点A1的坐标为（1，2），画出平移后的线段A1B1，并写出点B1的坐标为 ．
经过点A（﹣1，0）和点B（4，0），且与y轴交于点C，点D的坐标为（2，0），点P（m，n）是该抛物线上的一个动点，连接CA，CD，PD，PB．
粤公网安备 44130202000953号