已知椭圆C：
+
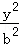=1（a＞b＞0）的两个焦点分别为F1（﹣2，0），F2（2，0），离心率为
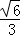．过焦点F2的直线l（斜率不为0）与椭圆C交于A，B两点，线段AB的中点为D，O为坐标原点，直线OD交椭圆于M，N两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）当四边形MF1NF2为矩形时，求直线l的方程．
相关试题
（
为实常数）。
时，证明：
不是奇函数；
与
的值；
.
，且
有最小值2时，求
的值；
时，有
恒成立，求实数
的取值范围.
,q: 
,若
是
的必要不
是定义在（－∞，+∞）上的函数，对一切
均
，且当
时，
，求当
时，推荐套卷
已知椭圆C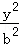：+=1（a＞b＞0）的两个焦点分别为F1（﹣2，0），F2（2，0），离心率为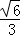．过焦点F2的直线l（斜率不为0）与椭圆C交于A，B两点，线段AB的中点为D，O为坐标原点，直线OD交椭圆于M，N两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）当四边形MF1NF2为矩形时，求直线l的方程．
粤公网安备 44130202000953号