设函数的集合P＝{f（x）＝log2（x＋a）＋b|a＝－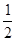
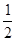，0，，1；b＝－1，0，1}，平面上点的集合Q＝{（x，y）|x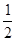＝－，0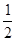，，1；y＝－1，0，1}，则在同一直角坐标系中，P中函数f（x）的图像恰好经过Q中两个点的函数的个数是（ ）
| A．6 | B．4 | C．8 | D．10 |
的渐近线方程是（）
”是“
” 的（）
与函数
的零点分别为
和
（）
的图象沿
轴向左平移
个单位
后图象的一个对称中心是
，则
，
，
，则（）
推荐套卷
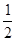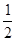设函数的集合P＝{f（x）＝log2（x＋a）＋b|a＝－，0，，1；b＝－1，0，1}，平面上点的集合Q＝{（x，y）|x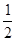＝－，0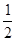，，1；y＝－1，0，1}，则在同一直角坐标系中，P中函数f（x）的图像恰好经过Q中两个点的函数的个数是（ ）
| A．6 | B．4 | C．8 | D．10 |
粤公网安备 44130202000953号