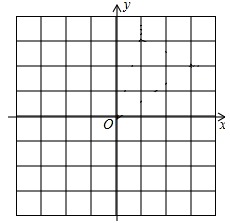
如图，在边长为1的小正方形组成的网格中，A、B两点均在格点上，且坐标分别为A（3，2）；B（1，3）．
（1）点B关于y轴对称的点的坐标为 ．
（2）在网格线中描出点A、B，并画出△AOB，若将△AOB向左平移3个单位，再向上平移2个单位得到△A1O1B1，则点A1点坐标为 ．
相关试题
，
，求
；
，
，求
（用m、n表示）.
的边
在
的边
上，顶点
、
分别在边
、
上，
，垂足为
．已知
，
.
为正方形时，求该正方形的边长；
面积为18时，求矩形的长和宽．
中，
，
，
，求（1）
的值. 
中，
、
、
分别是
、AC、BC上的点，联结
、EF交于点G，且
.
相似的三角形（不用证明）；
，试求
的值．
. 求证：(1)
；(2) 
．
相关知识点
推荐套卷
如图，在边长为1的小正方形组成的网格中，A、B两点均在格点上，且坐标分别为A（3，2）；B（1，3）．
（1）点B关于y轴对称的点的坐标为 ．
（2）在网格线中描出点A、B，并画出△AOB，若将△AOB向左平移3个单位，再向上平移2个单位得到△A1O1B1，则点A1点坐标为 ．
粤公网安备 44130202000953号