已知抛物线方程为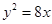 ,
,
(1)直线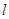 过抛物线的焦点
过抛物线的焦点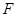 ,且垂直于
,且垂直于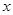 轴,
轴,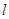 与抛物线交于
与抛物线交于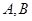 两点,求
两点,求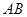 的长度。
的长度。
(2)直线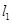 过抛物线的焦点
过抛物线的焦点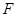 ,且倾斜角为
,且倾斜角为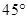 ,直线
,直线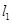 与抛物线相交于
与抛物线相交于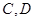 两点,
两点,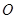 为原点。求△
为原点。求△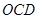 的面积。
的面积。
相关知识点
推荐套卷
已知抛物线方程为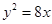 ,
,
(1)直线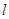 过抛物线的焦点
过抛物线的焦点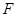 ,且垂直于
,且垂直于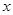 轴,
轴,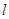 与抛物线交于
与抛物线交于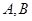 两点,求
两点,求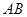 的长度。
的长度。
(2)直线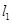 过抛物线的焦点
过抛物线的焦点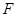 ,且倾斜角为
,且倾斜角为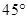 ,直线
,直线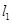 与抛物线相交于
与抛物线相交于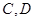 两点,
两点,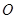 为原点。求△
为原点。求△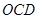 的面积。
的面积。