以下四个关于圆锥曲线的命题中：
①双曲线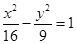
与椭圆
有相同的焦点；
②在平面内，设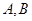
为两个定点，
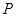为动点，且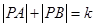
，其中常数
为正实数，则动点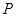的轨迹为椭圆；
③方程
的两根可分别作为椭圆和双曲线离心率；
④过双曲线
的右焦点
作直线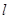
交双曲线与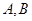两点，若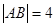
，则这样的直线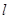有且仅有3条．
其中真命题的序号为 ．
满足
，设
．
是等比数列；
，求
的最小值．
，
满足约束条件
，且
有最大值
，则实数
．
且
，则
的最小值是 ，
的最小值是 ．
中，若
，则
．
不等式
的解集是 ．相关知识点
推荐套卷
以下四个关于圆锥曲线的命题中：
①双曲线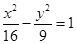与椭圆有相同的焦点；
②在平面内，设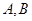为两个定点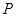，为动点，且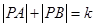，其中常数为正实数，则动点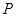的轨迹为椭圆；
③方程的两根可分别作为椭圆和双曲线离心率；
④过双曲线的右焦点作直线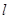交双曲线与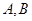两点，若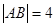，则这样的直线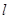有且仅有3条．
其中真命题的序号为 ．
粤公网安备 44130202000953号