如图：A、B两城相距100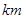 
，某天燃气公司计划在两地之间建一天燃气站D 给A、B两城供气．已知D地距A城
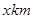，为保证城市安全，天燃气站距两城市的距离均不得少于10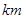．已知建设费用
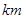（万元）与A、B两地的供气距离（）的平方和成正比，当天燃气站D距A城的距离为40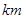时, 建费用为1300万元．（供气距离指天燃气站距到城市的距离）
（1）把建设费用（万元）表示成供气距离
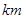（）的函数，并求定义域；
（2）天燃气供气站建在距A城多远，才能使建设供气费用最小，最小费用是多少？
推荐套卷
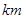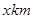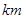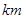如图：A、B两城相距100 ，某天燃气公司计划在两地之间建一天燃气站D 给A、B两城供气．已知D地距A城，为保证城市安全，天燃气站距两城市的距离均不得少于10．已知建设费用（万元）与A、B两地的供气距离（）的平方和成正比，当天燃气站D距A城的距离为40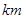时, 建费用为1300万元．（供气距离指天燃气站距到城市的距离）
（1）把建设费用（万元）表示成供气距离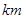（）的函数，并求定义域；
（2）天燃气供气站建在距A城多远，才能使建设供气费用最小，最小费用是多少？
粤公网安备 44130202000953号