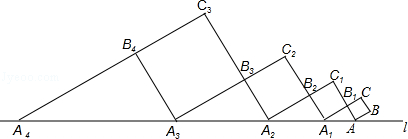
如图，正方形ABCB1中，AB1．AB与直线l的夹角为30°_优题课试题网

首页 / 初中数学 / 试题详细

更新 2022-09-03
科目数学
题型填空题
难度较难
浏览 2094

如图，正方形ABCB₁中，AB=1．AB与直线l的夹角为30°，延长CB₁交直线l于点A₁，作正方形A₁B₁C₁B₂，延长C₁B₂交直线l于点A₂，作正方形A₂B₂C₂B₃，延长C₂B₃交直线l于点A₃，作正方形A₃B₃C₃B₄，…，依此规律，则A₂₀₁₄A₂₀₁₅= ．

登录免费查看答案和解析

相关试题

如图所示，∠1=∠2，∠3=116°，则∠4=_________度。

题型：未知
难度：未知

收藏答案/解析

如图，已知a∥b，∠1=75°，则∠2=_________度。

题型：未知
难度：未知

收藏答案/解析

一个角的补角加上等于这个角的余角的5倍，则这个角为 _________。

题型：未知
难度：未知

收藏答案/解析

计算：90°-24°16′42″= _________。

题型：未知
难度：未知

收藏答案/解析

计算：13°27′33"+76°32′27" =_________。

题型：未知
难度：未知

收藏答案/解析

相关知识点

相似多边形的性质

推荐套卷

热门套卷

粤ICP备20024846号

粤公网安备

粤公网安备 44130202000953号

Copyright ©2020-2025 优题课 youtike.com 版权所有 Powered by：Youtike Platform 6.8.8

声明：本网站部分内容由互联网用户自发贡献自行上传，本网站不拥有所有权，也不承担相关法律责任。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。