已知函数f（x）=alnx+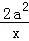
+x（a≠0）．
（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线与直线x﹣2y=0垂直，求实数a的值；
（Ⅱ）讨论函数f（x）的单调性；
（Ⅲ）当a∈（﹣∞，0）时，记函数f（x）的最小值为g（a），求证：g（a）≤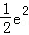
．
相关试题
，
且
的定义域； 
的奇偶性，并予以证明；
的定义域；
的值域；
，求
的单调递减区间。
在区间
上单调递减，求实数
的取值范围。
,
，
，（1）求
；（2）求
推荐套卷
已知函数f（x）=alnx+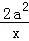+x（a≠0）．
（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线与直线x﹣2y=0垂直，求实数a的值；
（Ⅱ）讨论函数f（x）的单调性；
（Ⅲ）当a∈（﹣∞，0）时，记函数f（x）的最小值为g（a），求证：g（a）≤．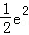
粤公网安备 44130202000953号