数学课代表剪了两张直角三角形纸片,进行了如下的操作: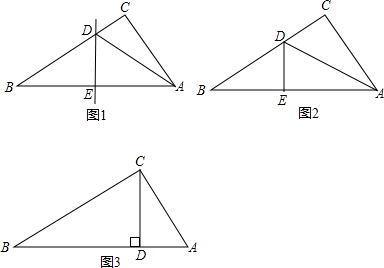
操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为 DE.
(1)如果AC=6,BC=8,则△ACD周长为__________;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为____________;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AB重合。
(3)若AC=9cm,BC=12cm,请求出CD的长.
相关知识点
推荐套卷
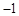 ,那么
,那么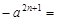 _________.
_________.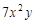 与
与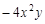 的差是 .
的差是 . 的系数为_______,次数为_______.
的系数为_______,次数为_______. ,9,0.01,
,9,0.01, ,0,
,0, 这些数中,负有理数的个数是______.
这些数中,负有理数的个数是______.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号