如图，△ABC是边长为4cm的等边三角形，AD为BC边上的高，点P沿BC向终点C运动，速度为1cm/s，点Q沿CA、AB向终点B运动，速度为2cm/s，若点P、Q两点同时出发，设它们的运动时间为x（s）．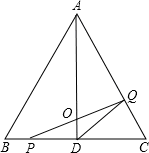
（l）求x为何值时，PQ⊥AC；x为何值时，PQ⊥AB？
（2）当O＜x＜2时，AD是否能平分△PQD的面积？若能，说出理由；
（3）探索以PQ为直径的圆与AC的位置关系，请写出相应位置关系的x的取值范围（不要求写出过程）．
相关试题
如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，求证DF∥AC.
证明：∵∠1=∠2（已知）
∠2=∠3，∠1="∠4" （）
∴∠3=∠4（等量代换）
∴_____∥_____ ( )
∴∠C=∠ABD ( )
∵∠C=∠D (已知 )
∴∠D=∠ABD (等量代换 )
∴DF∥AC
、3，点P为数轴上一动点，其对应的数为x.
推荐套卷
粤公网安备 44130202000953号