如图，在RtΔABC中，∠C=90º，AC=4cm，BC=3cm．动点M、N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A、B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动。连接PM、PN。设移动时间为t（单位：秒，0<t<2．5）．
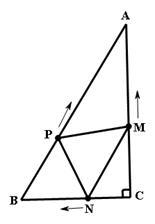
（1）当t为何值时，以A、P、M为顶点的三角形与ΔABC相似？
（2）是否存在某一时刻t，使△PMN 的面积恰好是△ABC 面积的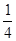
；若存在求t的值；若不存在，请说明理由．
相关试题
（本小题满分8分）
“知识改变命运，科技繁荣祖国”．我市中小学每年都要举办一届科技运动会．下图为我市某校2011年参加科技运动会航模比赛（包括空模、海模、车模、建模四个类别）的参赛人数统计图：
 |
（1）该校参加车模、建模比赛的人数分别是人和人；
（2）该校参加航模比赛的总人数是人，空模所在扇形的圆心角的度数是°，
并把条形统计图补充完整；
（3）从全市中小学参加航模比赛选手中随机抽取80人，其中有32人获奖．今年我市中小学参加航模比赛人数共2485人，请你估算今年参加航模比赛的获奖人数约是多少人?
(2)、
(4)、 
(6)、
)-1 - 2sin 45°+ |1-
|．相关知识点
推荐套卷
粤公网安备 44130202000953号