新规定这样一种运算法则：a△b=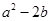
，如2△3=
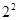－2×3=4－6=－2；
利用运算法则解决下列问题：
（1）1△2= ，（－1）△［1△（－1）］ = ．
（2）若2△x=3，求x的值．
（3）若（－2）△x=－2+x，求x的值．
推荐套卷
新规定这样一种运算法则：a△b=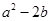，如2△3=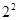－2×3=4－6=－2；
利用运算法则解决下列问题：
（1）1△2= ，（－1）△［1△（－1）］ = ．
（2）若2△x=3，求x的值．
（3）若（－2）△x=－2+x，求x的值．
粤公网安备 44130202000953号