某商店计划每天购进某商品若干件,商店每销售一件该商品可获利润50元.供大于求时,剩余商品全部退回,但每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(1)若商店一天购进该商品10件,求当天的利润 (单位:元)关于当天需求量
(单位:元)关于当天需求量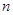 (单位:件,
(单位:件,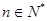 )的函数解析式;
)的函数解析式;
(2)商店记录了50天该商品的日需求量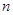 (单位:件),整理得下表:
(单位:件),整理得下表:
若商店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求该商品一天的利润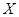 的分布列及平均值.
的分布列及平均值.
推荐套卷
某商店计划每天购进某商品若干件,商店每销售一件该商品可获利润50元.供大于求时,剩余商品全部退回,但每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(1)若商店一天购进该商品10件,求当天的利润 (单位:元)关于当天需求量
(单位:元)关于当天需求量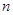 (单位:件,
(单位:件,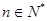 )的函数解析式;
)的函数解析式;
(2)商店记录了50天该商品的日需求量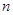 (单位:件),整理得下表:
(单位:件),整理得下表:
若商店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求该商品一天的利润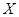 的分布列及平均值.
的分布列及平均值.