如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,﹣2).直线OM是一次函数y=x的图像.让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t.
(1)填空
①直线OM与x轴所夹的锐角度数为 °;
②当t= 时,⊙A与坐标轴有两个公共点;
(2)当t>3时,求出运动过程中⊙A与直线OM相切时的t的值;
(3)运动过程中,当⊙A与直线OM相交所得的弦长为1时,求t的值.

相关知识点
推荐套卷
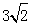 m,求点B到地面的垂直距离BC.
m,求点B到地面的垂直距离BC.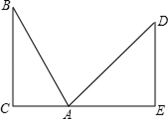
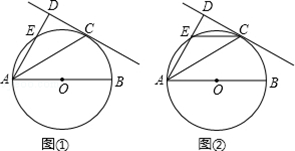
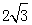 ,则(1)中画出的正方形E′F′P′N′的边长为.
,则(1)中画出的正方形E′F′P′N′的边长为.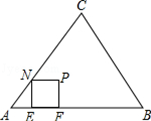
 粤公网安备 44130202000953号
粤公网安备 44130202000953号