（本大题满分12分）如图所示，有一块半径为
的半圆形钢板，设计剪裁成矩形ABCD的形状，它的边
在圆O的直径上，边CD的端点在圆周上，若设矩形的边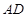
为
；
（1）将矩形的面积
表示为关于的函数，并求其定义域；
（2）求矩形面积的最大值及此时边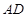的长度．
的前
项和为
，已知
成等差数列．
;
，问
是数列
的等比数列
中，
，前三项的和为
．
，设数列
满足
，
，求使
的
的最小值．
的解集为是
，
的值
的解集．
中，
，
，求
．推荐套卷
（本大题满分12分）如图所示，有一块半径为的半圆形钢板，设计剪裁成矩形ABCD的形状，它的边在圆O的直径上，边CD的端点在圆周上，若设矩形的边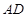为；
（1）将矩形的面积表示为关于的函数，并求其定义域；
（2）求矩形面积的最大值及此时边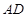的长度．
粤公网安备 44130202000953号