（贵港）如图，抛物线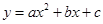
与x轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴l为
．
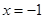（1）求抛物线的解析式并写出其顶点坐标；
（2）若动点P在第二象限内的抛物线上，动点N在对称轴l上．
①当PA⊥NA，且PA=NA时，求此时点P的坐标；
②当四边形PABC的面积最大时，求四边形PABC面积的最大值及此时点P的坐标．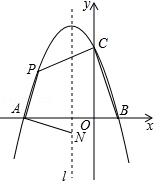
相关试题
（贵港）如图，抛物线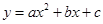与x轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴l为．
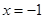（1）求抛物线的解析式并写出其顶点坐标；
（2）若动点P在第二象限内的抛物线上，动点N在对称轴l上．
①当PA⊥NA，且PA=NA时，求此时点P的坐标；
②当四边形PABC的面积最大时，求四边形PABC面积的最大值及此时点P的坐标．
的式子表示你所发现的规律；
(结果可以保留幂的形式)
和
的平方根又是多少？
G的边长
粤公网安备 44130202000953号